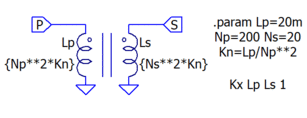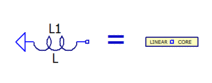Difference between revisions of "Transformers"
m (Reverted edits by Lewispaul (talk) to last revision by Analogspiceman) (Tag: Rollback) |
|||
| (175 intermediate revisions by 15 users not shown) | |||
| Line 1: | Line 1: | ||
== Transformers == | == Transformers == | ||
| − | + | === Introduction === | |
| − | Although it is very possible | + | Do you wish to study the behavior of transformers and inductors and explore their mysteries? LTspice is the ideal learning tool for this purpose. LTspice will faithfully model both ideal and real magnetic devices. However, caution is advised when first experimenting with unfamiliar concepts in inductors and transformers. Be sure to minimize simulation problems by including reasonably realistic parasitic resistances (both series and parallel) directly into each inductor, whether used individually or as part of a transformer. |
| + | |||
| + | A good learning and reference resource is the [http://coefs.uncc.edu/mnoras/files/2013/03/Transformer-and-Inductor-Design-Handbook_Chapter_17.pdf <i>Transformer and Inductor Design Handbook</i> Chapter 17, Winding Capacitance and Leakage Inductance] 4th Edition by Colonel William. T. McLyman. Mike Engelhardt, the author of LTspice, explains how to make transformers in LTspice in a [https://www.analog.com/en/technical-articles/using-transformers-in-ltspice-switcher-cadiii.html 2006 LT-Magazine article]. | ||
| + | |||
| + | Always keep in mind that starting a simulation with a dc voltage bias on an inductor or transformer winding will cause an initial inductor current only limited by the inductor's series resistance (this would be like trying to initialize an ideal capacitor with a current source - no matter how small the source, the dc voltage will increase without bounds - or at least until the capacitor breaks down). In fact, if you are like most engineers, you are much more comfortable with the behavior of capacitors. If so, use this to your advantage by applying duality to think of what to expect when dealing with inductors. | ||
| + | |||
| + | === How do I make a transformer in LTspice? === | ||
| + | |||
| + | [[File:LTspice_Transformer.gif|right|179x143px|Two lines were used to draw the core]] | ||
| + | |||
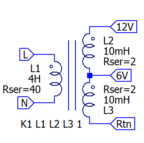
| + | Although it is very possible to make a dedicated subcircuit for a specific transformer, the preferred method of making a generic transformer when drafting a simulation schematic is to simply place a separate inductor for each separate transformer winding and then couple them all together magnetically via a single ''[[Mutual Inductance]] (K) statement'' placed as a [[SPICE Directive]] on the schematic. Note that inductors called out in a [[Mutual Inductance]] statement will be automatically given a phasing dot if one does not already exist. | ||
K1 L1 L2 L3 1 ; causes phasing dots to automatically appear on L1-L3 inductor symbols | K1 L1 L2 L3 1 ; causes phasing dots to automatically appear on L1-L3 inductor symbols | ||
| − | When creating a new transformer this way, especially for use in a switched-mode power circuit, it is generally best to first specify the mutual coupling coefficient to be exactly unity. By starting with | + | When creating a new transformer this way, especially for use in a switched-mode power circuit, it is generally best to first specify the mutual coupling coefficient to be exactly unity. By starting with unity coupling there will be no leakage inductance in any winding and this will minimize the likelihood of the windings ringing at extremely high frequencies (which can slow the simulation to a crawl at each switching edge). However, be aware that a mutual inductance value of plus (or minus) unity ''may'' lead to simulation difficulties if ''Skip-the-initial-operating-point-solution'' (UIC) is specified for the .tran command. Prevent this by specifying a realistic resistance for each inductor "winding" (ctrl-right-mouse-click). Note that when coupled inductors are used as transformer windings, individual winding inductances rather than turns ratios must be specified (''inductance ratios should be set to be proportional to <u>the '''square''' of the turns ratios''</u>). |
| + | |||
| + | === I've created an ideal transformer so it should work at all frequencies, even including DC, right? === | ||
| + | |||
| + | No, but lots of users completely misunderstand or overlook this when setting up their simulation. This common mistake can lead to a lot of needless doubt following unexpected and puzzling simulation results produced by LTspice when presented with an ideal transformer that is inadvertently initialized with a large amount of dc voltage applied to its windings. This is probably the most common self-inflicted pitfall that trips up users improperly specifying ac voltage sources. | ||
| + | |||
| + | When LTspice calculates initial conditions for voltage sources, it uses the values at time = 0. Depending on the starting phase angle and delay specified for a sine source, this can be as much as the voltage at the peak of the sine wave. When the simulator attempts to find the circuit's initial solution, this is the equivalent to hooking the transformer up to a large dc voltage source. Current will only be limited by winding resistance (which, in the ideal case, may be zero). Note that a real transformer will saturate at a relatively low current and would normally not store much energy (it would also probably burn up with so much dc applied), but an ideal transformer with an ideal magnetizing inductance may store a physically impossible amount of simulated "virtual" energy. | ||
| + | |||
| + | Without realizing it, many users may instruct LTspice to initialize the transformer magnetizing inductance with huge starting currents. Since they have used an ideal inductance that does not saturate (like a real transformer would), it starts out with dc current that may take many hundreds of line (or switching) cycles to die away. This completely unrealistic energy source then may dominate the simulation, causing strange and unexpectedly puzzling behavior. In such cases, LTspice is just innocently following the instructions given it and accurately computing the unrealistic results (garbage in, garbage out). | ||
| + | |||
| + | To avoid this bogus and unwanted result, you must either arrange '''''the ac source to be zero at time zero''''' or '''''instruct LTspice not to use a dc solution for the starting point (UIC).''''' | ||
| + | |||
| + | === I want to model leakage inductance - how should I do that? === | ||
| + | |||
| + | The most flexible method is to keep the windings' mutual inductance statement at unity and add a small discrete leakage inductance in series with each winding. This is the most straightforward way to model transformers with asymmetrical leakage inductances. However, if your transformer is electrically symmetrical, it may be more convenient to simply set the mutual inductance to a value less than one. For each winding the resulting leakage inductance will be (1-K) times that winding's inductance. Also, each winding's coupled inductance also will decrease to K times that winding's inductance, but for typical values of K (>>0.9) this effect will be very small. Note that physical transformer leakage inductance measured in the laboratory typically is close to the sum of the leakage inductance of two windings in series combination (with coupled inductance and perhaps several windings partially in parallel). | ||
| + | |||
| + | '''This is how LTspice "sees" coupled inductors:''' | ||
| + | |||
| + | For n inductors coupled together with a K statement, each inductor L1 through Ln is divided into two parts, a completely non-coupled "leakage" inductance equal to (1-K)*Lx (where Lx is the particular inductor in question) and a completely coupled "mutual" inductance equal to K*Lx. Voltage and current ratios of the coupled parts are related by the ratio of the square root of the the inductances L1 through Ln (this is the apparent "turns ratio"). | ||
| + | |||
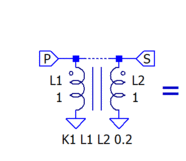
| + | [[File:Loosely_Coupled_Transformer.gif|right|186px|(full: 371x322)|Coupling is only K=0.2]] | ||
| + | |||
| + | * For example, given two inductors coupled by a K statement: | ||
| + | L1 1 0 1H | ||
| + | L2 2 0 1H | ||
| + | K1 L1 L2 0.2 | ||
| + | |||
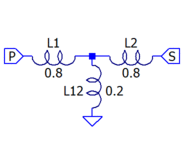
| + | [[File:Loosely_Coupled_Equivalent.gif|right|185px|(full: 370x312)|"Winding" inductance is 1H]] | ||
| + | |||
| + | * In LTspice, this is the same as: | ||
| + | L1 1 12 0.8H | ||
| + | L12 12 0 0.2H | ||
| + | L2 2 12 0.8H | ||
| + | |||
| + | Other engineering conventions regarding the definition of K, coupling and formula for leakage inductance are irrelevant to LTspice. Other formula for leakage inductance are intended to find total leakage inductance from an input winding through to an output winding(s) rather than the partial leakage inductance for each individual winding. | ||
| + | |||
| + | === How about transformer saturation effects? Can LTspice model those? === | ||
| + | |||
| + | Yes, LTspice comes with a non-linear hysteretic core model built in! This is the 1991 model by John Chan et al. Compared to older core models, [[the Chan model]] is particularly robust, computationally efficient and compact, requiring only three parameters to define most any commonly encountered magnetic hysteresis loop. (LTspice also allows building an arbitrary inductance based on self flux and/or any valid function of node voltages and branch currents. [[The Arbitrary Inductor model|The arbitrary inductor model]] can be very efficiently used to create saturation without hysteresis.) | ||
| + | |||
| + | Once the Chan core material's generic magnetic properties are set, establishing the circuit-level non-linear inductance requires specifying three more parameters to set the geometry of the specific core and specifying one additional parameter for the core winding turn-count. The Chan inductor <font color="green" title="(has been mentioned as a possibility for a future release)">does not currently</font> directly support [[Mutual Inductance]], so unless only a single-winding inductor is being modeled, multiple windings must be added via additional circuitry. The simplest way to do this is to construct an ideal, unity coupled transformer with as many windings as required and then put the Chan inductor directly in parallel with any one of the windings (taking care to set the turns to match that particular winding). Since the magnetic effects (including non-saturated inductance) are already modeled by the Chan inductor, the inductance of the transformer's parallel winding must be enough larger (>>10) not to significantly load the Chan inductance. As before, the inductances for the other windings should be scaled by the square of their individual turns ratios (with respect to the paralleled winding). | ||
| + | |||
| + | === Okay, but calculating winding inductances is tedious. Is there some way to just enter a turns count for all the windings? === | ||
| + | |||
| + | Yes, this can be done in any of a number of ways. For example, the values for each of the inductances may be directly parametrized via <font color="green"><b title="Lx node1 node2 {Lm*(Nx/Nm)**2}">curly braces</b></font> to be a function of turns ratios (squared), or a subcircuit that accepts turns as a parameter may be used to encapsulate the windings implementation details. | ||
| + | |||
| + | * Use parameters to to convert input of winding turns to inductance: | ||
| + | [[File: Parameterized_Transformer.gif|right|307px|(full: 613x236)|Turns are entered as parameters from which the inductance is calculated]] | ||
| + | .param Lp=20m Np=200 Ns=20 ; inputs: primary inductance, primary turns, secondary turns | ||
| + | .param Kn=Lp/Np**2 ; calculated inductance per turn squared | ||
| + | Lp 1 0 {Np**2*Kn} ; primary inductance = 200t**2*Kn | ||
| + | Ls 2 0 {Ns**2*Kn} ; secondary inductance = 20t**2*Kn | ||
| + | Kx Lp Ls 1 ; core coupling factor = 1 | ||
| + | |||
| + | Below is a schematic of a simple LTspice subcircuit that is functionally equivalent to a winding (without a core). Its symbol appears just to the right of the schematic. LTspice's fully extended inductor parasitics are included within this model. Observe that the winding is presented with a voltage equal to the core's volts/turn*primary_turns and that the core is presented with a current equal to the winding's ampere-turns = winding's amps*primary_turns. Also note if the leakage inductance and resistances are zero, the winding is completely floating with respect to the core and that the winding performs a voltage ratio transformation (set by the turns ratio) from DC to light. | ||
| + | |||
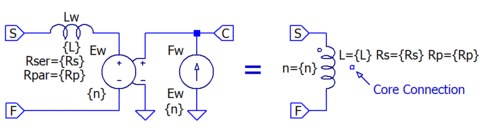
| + | * First, the basic winding: Start (dot), Finish, Core: | ||
| + | [[File: Simple Winding Symbol & Subcircuit.gif|right|480px|(full: 959x270)|This simple subcircuit is equivalent to an inductor or transformer winding]] | ||
| + | .subckt Winding s f c params: n=100 L=1u Rs=1m Rp=100 | ||
| + | Lw s 1 {L} Rser={Rs} Rpar={Rp} ; leakage and resistance | ||
| + | Ew 1 f c 0 {n} ; impose core volts/turn*turns onto winding | ||
| + | Fw 0 c Ew {n} ; impose winding amperes*turns onto core | ||
| + | .ends Winding | ||
| + | |||
| + | |||
| + | === DC to DC Transformer (no magnetizing inductance - no energy storage) === | ||
| + | |||
| + | The transformer winding subcircuits are DC coupled and, when connected to a "core" (1TΩ in parallel with 1pF) that supports DC without drawing current, they combine to make a transformer that draws no magnetizing current, stores no energy and therefore is immune to errant initial conditions. This model may be an advantage when first experimenting with new power circuits. | ||
| + | |||
| + | For better cosmetics the simple DC core may encapsulated in its own subcircuit and symbol. | ||
| + | |||
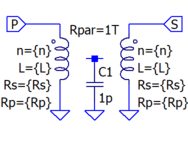
| + | [[File: DC_to_DC_Transformer.gif|right|188px|(full: 376x288)|DC to DC (because of "core") transformer with two windings]] | ||
| + | * Here is a DC "core" that does not draw increasing current with time: | ||
| + | .subckt Core_DC C | ||
| + | Cc C 0 1p Rpar=1T ; dump the "core's" ampere-turns into a small conductance | ||
| + | .ends Core_DC | ||
| + | |||
| + | [[File: DC_to_DC_Transformer_&_Core.gif|right|186px|(full: 372x266)|DC to DC transformer with DC core symbol for aesthetics]] | ||
| + | * DC-to-DC Transformer Equivalent (Netlist Uprocessed): | ||
| + | Xp P 0 C Winding n=1 L=1u Rs=1m Rp=100 ; primary winding of 1:1 transformer | ||
| + | Xs S 0 C Winding n=1 L=1u Rs=1m Rp=100 ; secondary winding of 1:1 transformer | ||
| + | Xc C CoreDC ; subcircuit consisting of 1TΩ in parallel with 1pF | ||
| + | |||
| + | === Linear Transformer (linear magnetizing inductance - potentially unlimited energy storage) === | ||
| + | |||
| + | A standard linear transformer may easily be created simply by changing the core to be a standard inductor with Rs=0. In this form (with a standard ''linear'' magnetizing inductance "core") the model is mostly useful as a perceptual window into the way coupled inductors work in LTspice since linear transformers are more easily and simply built with standard coupled inductors. Note that the magnetizing inductance "core" is the single summing point for the ''ampere-turns'' from all the windings and is the sole source of ''impressed voltage'' (=L*di/dt) reflected onto all the windings. Although this subcircuit is an unnecessary and overly complex representation for a transformer with a linear core inductance, it will be absolutely required if multiple windings are to be "wrapped" onto LTspice's nonlinear Chan inductance model, so take a moment to read it through (the Chan version will follow shortly). | ||
| + | |||
| + | |||
| + | * Parametize and wrap an inductor with a subcircuit: | ||
| + | [[File: Linear_Core.gif|right|212px|(full: 423x165)|A linear core is simply an inductor with Rser=0]] | ||
| + | .subckt Core_Linear C params: L=20m Rp=10k Cp=10p | ||
| + | Lc C 0 {L} Rser=0 Rpar={Rp} Cpar={Cp} | ||
| + | .ends Core_Linear | ||
| + | |||
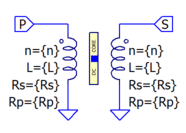
| + | [[File: Linear_Transformer.gif|right|187px|(full: 374x270)|Transformer with linear core]] | ||
| + | * Linear Transformer Equivalent (Netlist Unprocessed): | ||
| + | Xp P 0 C Winding n=1 L=1u Rs=1m Rp=100 ; primary winding of 1:1 transformer | ||
| + | Xs S 0 C Winding n=1 L=1u Rs=1m Rp=100 ; secondary winding of 1:1 transformer | ||
| + | Xc C Core_Linear L=20m Rp=10k Cp=10p ; subcircuit consisting of an inductor with Rs=0 | ||
| + | |||
| + | * Linear Transformer Equivalent (Netlist Flattened): | ||
| + | [[File: Linear_Transformer_Full.gif|right|455px|(full: 909x236)|Transformer with linear core]] | ||
| + | Lp Ps 1 1u Rser=1m Rpar=100 ; leakage and resistance | ||
| + | Ep 1 Pf C 0 1 ; impose core volts/turn*turns onto winding | ||
| + | Fp 0 C Ep 1 ; impose winding ampere*turns onto core | ||
| + | Lc C 0 20m Rpar=10k Cpar=10p ; liner inductor core (no magnetic saturation) | ||
| + | + Rser=0 ; Rser must equal zero | ||
| + | Fs 0 C Es 1 ; impose winding ampere*turns onto core | ||
| + | Es 1 Sf C 0 1 ; impose core volts/turn*turns onto winding | ||
| + | Ls Ss 1 1u Rser=1m Rpar=100 ; leakage and resistance | ||
| + | |||
| + | === Chan Transformer (saturating magnetizing inductance with hysteresis - limited energy storage) === | ||
| + | |||
| + | Now that the windings are separate from the core, a Chan inductor may simply be substituted for the linear inductor core. Since the inductance of a Chan inductor is not assigned, but is determined by its magnetic material, dimensional properties and winding turns, one must adjust inductance by iteratively adjusting the gap and/or winding turns. Measure inductancs by comparing slopes when subjected to the same stepped DC voltage. | ||
| − | + | * Parametize and wrap a Chan inductor with a subcircuit: | |
| + | [[File: Chan_Core.gif|right|170px|(full: 340x288)|Physical properties based core with hysteresis and saturation]] | ||
| + | .subckt Core_Chan C params: | ||
| + | + Bs=0.4 Br=0.1 Hc=20 ; Core default magnetic parameters | ||
| + | + A=25u1 Lm=19m8 Lg=0m7 ; Core default physical parameters | ||
| + | + Rp=10k Cp=10p ; Core default parallel loss and capacitance | ||
| + | Lc C 0 Rser=0 n=1 ; force Rser=0 and n=1 | ||
| + | + Bs={Bs} Br={Br} Hc={Hc} | ||
| + | + A={A} Lm={Lm} Lg={Lg} | ||
| + | + Rpar={Rp} Cpar={Cp} | ||
| + | .ends Core_Chan | ||
| − | + | [[File: Chan_Transformer.gif|right|172px|(full: 344x276)|Physically parameterized transformer with hysteresis and saturation]] | |
| + | * Chan Transformer Equivalent (Netlist Unprocessed): | ||
| + | Xp P 0 C Winding n=100 L=1u Rs=1m Rp=100 ; primary winding of 1:1 transformer | ||
| + | Xs S 0 C Winding n=100 L=1u Rs=1m Rp=100 ; secondary winding of 1:1 transformer | ||
| + | Xc C Core_Chan ; Chan inductor subcircuit with forced Rs=0 and n=1 | ||
| + | + Bs=0.4 Br=0.1 Hc=20 Br=.10 ; Assigned core magnetic parameters | ||
| + | + A=25u1 Lm=19m8 Lg=0m7 ; Assigned core physical parameters | ||
| + | + Rp=10k Cp=10p ; Assigned core parallel loss and capacitance | ||
| + | === Now how do I plot a B-H curve to see the Chan model's hysteresis-saturation curves? === | ||
| − | + | Plotting hysteresis-saturation curves of the Chan Transformer in LTspice | |
| − | + | ''Under construction.'' | |
| − | + | 1 ampere∙turn/meter = 4∙π/1000 Oersted(Oe) | |
| + | 1 volt∙seconds/turn/meter² = 1 Tesla(T) = 10,000 gauss(G) | ||
| − | |||
| − | + | {{#widget:DISQUS | |
| + | |id=ltwiki | ||
| + | |uniqid={{PAGENAME}} | ||
| + | |url={{fullurl:{{PAGENAME}}}} | ||
| + | }} | ||
Latest revision as of 14:14, 17 May 2020
Contents
- 1 Transformers
- 1.1 Introduction
- 1.2 How do I make a transformer in LTspice?
- 1.3 I've created an ideal transformer so it should work at all frequencies, even including DC, right?
- 1.4 I want to model leakage inductance - how should I do that?
- 1.5 How about transformer saturation effects? Can LTspice model those?
- 1.6 Okay, but calculating winding inductances is tedious. Is there some way to just enter a turns count for all the windings?
- 1.7 DC to DC Transformer (no magnetizing inductance - no energy storage)
- 1.8 Linear Transformer (linear magnetizing inductance - potentially unlimited energy storage)
- 1.9 Chan Transformer (saturating magnetizing inductance with hysteresis - limited energy storage)
- 1.10 Now how do I plot a B-H curve to see the Chan model's hysteresis-saturation curves?
Transformers
Introduction
Do you wish to study the behavior of transformers and inductors and explore their mysteries? LTspice is the ideal learning tool for this purpose. LTspice will faithfully model both ideal and real magnetic devices. However, caution is advised when first experimenting with unfamiliar concepts in inductors and transformers. Be sure to minimize simulation problems by including reasonably realistic parasitic resistances (both series and parallel) directly into each inductor, whether used individually or as part of a transformer.
A good learning and reference resource is the Transformer and Inductor Design Handbook Chapter 17, Winding Capacitance and Leakage Inductance 4th Edition by Colonel William. T. McLyman. Mike Engelhardt, the author of LTspice, explains how to make transformers in LTspice in a 2006 LT-Magazine article.
Always keep in mind that starting a simulation with a dc voltage bias on an inductor or transformer winding will cause an initial inductor current only limited by the inductor's series resistance (this would be like trying to initialize an ideal capacitor with a current source - no matter how small the source, the dc voltage will increase without bounds - or at least until the capacitor breaks down). In fact, if you are like most engineers, you are much more comfortable with the behavior of capacitors. If so, use this to your advantage by applying duality to think of what to expect when dealing with inductors.
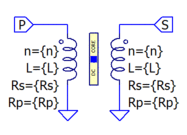
How do I make a transformer in LTspice?
Although it is very possible to make a dedicated subcircuit for a specific transformer, the preferred method of making a generic transformer when drafting a simulation schematic is to simply place a separate inductor for each separate transformer winding and then couple them all together magnetically via a single Mutual Inductance (K) statement placed as a SPICE Directive on the schematic. Note that inductors called out in a Mutual Inductance statement will be automatically given a phasing dot if one does not already exist.
K1 L1 L2 L3 1 ; causes phasing dots to automatically appear on L1-L3 inductor symbols
When creating a new transformer this way, especially for use in a switched-mode power circuit, it is generally best to first specify the mutual coupling coefficient to be exactly unity. By starting with unity coupling there will be no leakage inductance in any winding and this will minimize the likelihood of the windings ringing at extremely high frequencies (which can slow the simulation to a crawl at each switching edge). However, be aware that a mutual inductance value of plus (or minus) unity may lead to simulation difficulties if Skip-the-initial-operating-point-solution (UIC) is specified for the .tran command. Prevent this by specifying a realistic resistance for each inductor "winding" (ctrl-right-mouse-click). Note that when coupled inductors are used as transformer windings, individual winding inductances rather than turns ratios must be specified (inductance ratios should be set to be proportional to the square of the turns ratios).
I've created an ideal transformer so it should work at all frequencies, even including DC, right?
No, but lots of users completely misunderstand or overlook this when setting up their simulation. This common mistake can lead to a lot of needless doubt following unexpected and puzzling simulation results produced by LTspice when presented with an ideal transformer that is inadvertently initialized with a large amount of dc voltage applied to its windings. This is probably the most common self-inflicted pitfall that trips up users improperly specifying ac voltage sources.
When LTspice calculates initial conditions for voltage sources, it uses the values at time = 0. Depending on the starting phase angle and delay specified for a sine source, this can be as much as the voltage at the peak of the sine wave. When the simulator attempts to find the circuit's initial solution, this is the equivalent to hooking the transformer up to a large dc voltage source. Current will only be limited by winding resistance (which, in the ideal case, may be zero). Note that a real transformer will saturate at a relatively low current and would normally not store much energy (it would also probably burn up with so much dc applied), but an ideal transformer with an ideal magnetizing inductance may store a physically impossible amount of simulated "virtual" energy.
Without realizing it, many users may instruct LTspice to initialize the transformer magnetizing inductance with huge starting currents. Since they have used an ideal inductance that does not saturate (like a real transformer would), it starts out with dc current that may take many hundreds of line (or switching) cycles to die away. This completely unrealistic energy source then may dominate the simulation, causing strange and unexpectedly puzzling behavior. In such cases, LTspice is just innocently following the instructions given it and accurately computing the unrealistic results (garbage in, garbage out).
To avoid this bogus and unwanted result, you must either arrange the ac source to be zero at time zero or instruct LTspice not to use a dc solution for the starting point (UIC).
I want to model leakage inductance - how should I do that?
The most flexible method is to keep the windings' mutual inductance statement at unity and add a small discrete leakage inductance in series with each winding. This is the most straightforward way to model transformers with asymmetrical leakage inductances. However, if your transformer is electrically symmetrical, it may be more convenient to simply set the mutual inductance to a value less than one. For each winding the resulting leakage inductance will be (1-K) times that winding's inductance. Also, each winding's coupled inductance also will decrease to K times that winding's inductance, but for typical values of K (>>0.9) this effect will be very small. Note that physical transformer leakage inductance measured in the laboratory typically is close to the sum of the leakage inductance of two windings in series combination (with coupled inductance and perhaps several windings partially in parallel).
This is how LTspice "sees" coupled inductors:
For n inductors coupled together with a K statement, each inductor L1 through Ln is divided into two parts, a completely non-coupled "leakage" inductance equal to (1-K)*Lx (where Lx is the particular inductor in question) and a completely coupled "mutual" inductance equal to K*Lx. Voltage and current ratios of the coupled parts are related by the ratio of the square root of the the inductances L1 through Ln (this is the apparent "turns ratio").
- For example, given two inductors coupled by a K statement:
L1 1 0 1H L2 2 0 1H K1 L1 L2 0.2
- In LTspice, this is the same as:
L1 1 12 0.8H L12 12 0 0.2H L2 2 12 0.8H
Other engineering conventions regarding the definition of K, coupling and formula for leakage inductance are irrelevant to LTspice. Other formula for leakage inductance are intended to find total leakage inductance from an input winding through to an output winding(s) rather than the partial leakage inductance for each individual winding.
How about transformer saturation effects? Can LTspice model those?
Yes, LTspice comes with a non-linear hysteretic core model built in! This is the 1991 model by John Chan et al. Compared to older core models, the Chan model is particularly robust, computationally efficient and compact, requiring only three parameters to define most any commonly encountered magnetic hysteresis loop. (LTspice also allows building an arbitrary inductance based on self flux and/or any valid function of node voltages and branch currents. The arbitrary inductor model can be very efficiently used to create saturation without hysteresis.)
Once the Chan core material's generic magnetic properties are set, establishing the circuit-level non-linear inductance requires specifying three more parameters to set the geometry of the specific core and specifying one additional parameter for the core winding turn-count. The Chan inductor does not currently directly support Mutual Inductance, so unless only a single-winding inductor is being modeled, multiple windings must be added via additional circuitry. The simplest way to do this is to construct an ideal, unity coupled transformer with as many windings as required and then put the Chan inductor directly in parallel with any one of the windings (taking care to set the turns to match that particular winding). Since the magnetic effects (including non-saturated inductance) are already modeled by the Chan inductor, the inductance of the transformer's parallel winding must be enough larger (>>10) not to significantly load the Chan inductance. As before, the inductances for the other windings should be scaled by the square of their individual turns ratios (with respect to the paralleled winding).
Okay, but calculating winding inductances is tedious. Is there some way to just enter a turns count for all the windings?
Yes, this can be done in any of a number of ways. For example, the values for each of the inductances may be directly parametrized via curly braces to be a function of turns ratios (squared), or a subcircuit that accepts turns as a parameter may be used to encapsulate the windings implementation details.
- Use parameters to to convert input of winding turns to inductance:
.param Lp=20m Np=200 Ns=20 ; inputs: primary inductance, primary turns, secondary turns
.param Kn=Lp/Np**2 ; calculated inductance per turn squared
Lp 1 0 {Np**2*Kn} ; primary inductance = 200t**2*Kn
Ls 2 0 {Ns**2*Kn} ; secondary inductance = 20t**2*Kn
Kx Lp Ls 1 ; core coupling factor = 1
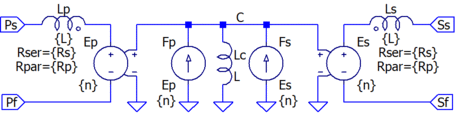
Below is a schematic of a simple LTspice subcircuit that is functionally equivalent to a winding (without a core). Its symbol appears just to the right of the schematic. LTspice's fully extended inductor parasitics are included within this model. Observe that the winding is presented with a voltage equal to the core's volts/turn*primary_turns and that the core is presented with a current equal to the winding's ampere-turns = winding's amps*primary_turns. Also note if the leakage inductance and resistances are zero, the winding is completely floating with respect to the core and that the winding performs a voltage ratio transformation (set by the turns ratio) from DC to light.
- First, the basic winding: Start (dot), Finish, Core:
.subckt Winding s f c params: n=100 L=1u Rs=1m Rp=100
Lw s 1 {L} Rser={Rs} Rpar={Rp} ; leakage and resistance
Ew 1 f c 0 {n} ; impose core volts/turn*turns onto winding
Fw 0 c Ew {n} ; impose winding amperes*turns onto core
.ends Winding
DC to DC Transformer (no magnetizing inductance - no energy storage)
The transformer winding subcircuits are DC coupled and, when connected to a "core" (1TΩ in parallel with 1pF) that supports DC without drawing current, they combine to make a transformer that draws no magnetizing current, stores no energy and therefore is immune to errant initial conditions. This model may be an advantage when first experimenting with new power circuits.
For better cosmetics the simple DC core may encapsulated in its own subcircuit and symbol.
- Here is a DC "core" that does not draw increasing current with time:
.subckt Core_DC C Cc C 0 1p Rpar=1T ; dump the "core's" ampere-turns into a small conductance .ends Core_DC
- DC-to-DC Transformer Equivalent (Netlist Uprocessed):
Xp P 0 C Winding n=1 L=1u Rs=1m Rp=100 ; primary winding of 1:1 transformer Xs S 0 C Winding n=1 L=1u Rs=1m Rp=100 ; secondary winding of 1:1 transformer Xc C CoreDC ; subcircuit consisting of 1TΩ in parallel with 1pF
Linear Transformer (linear magnetizing inductance - potentially unlimited energy storage)
A standard linear transformer may easily be created simply by changing the core to be a standard inductor with Rs=0. In this form (with a standard linear magnetizing inductance "core") the model is mostly useful as a perceptual window into the way coupled inductors work in LTspice since linear transformers are more easily and simply built with standard coupled inductors. Note that the magnetizing inductance "core" is the single summing point for the ampere-turns from all the windings and is the sole source of impressed voltage (=L*di/dt) reflected onto all the windings. Although this subcircuit is an unnecessary and overly complex representation for a transformer with a linear core inductance, it will be absolutely required if multiple windings are to be "wrapped" onto LTspice's nonlinear Chan inductance model, so take a moment to read it through (the Chan version will follow shortly).
- Parametize and wrap an inductor with a subcircuit:
.subckt Core_Linear C params: L=20m Rp=10k Cp=10p
Lc C 0 {L} Rser=0 Rpar={Rp} Cpar={Cp}
.ends Core_Linear
- Linear Transformer Equivalent (Netlist Unprocessed):
Xp P 0 C Winding n=1 L=1u Rs=1m Rp=100 ; primary winding of 1:1 transformer Xs S 0 C Winding n=1 L=1u Rs=1m Rp=100 ; secondary winding of 1:1 transformer Xc C Core_Linear L=20m Rp=10k Cp=10p ; subcircuit consisting of an inductor with Rs=0
- Linear Transformer Equivalent (Netlist Flattened):
Lp Ps 1 1u Rser=1m Rpar=100 ; leakage and resistance Ep 1 Pf C 0 1 ; impose core volts/turn*turns onto winding Fp 0 C Ep 1 ; impose winding ampere*turns onto core Lc C 0 20m Rpar=10k Cpar=10p ; liner inductor core (no magnetic saturation) + Rser=0 ; Rser must equal zero Fs 0 C Es 1 ; impose winding ampere*turns onto core Es 1 Sf C 0 1 ; impose core volts/turn*turns onto winding Ls Ss 1 1u Rser=1m Rpar=100 ; leakage and resistance
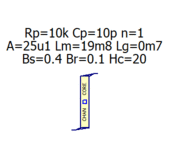
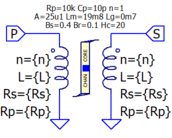
Chan Transformer (saturating magnetizing inductance with hysteresis - limited energy storage)
Now that the windings are separate from the core, a Chan inductor may simply be substituted for the linear inductor core. Since the inductance of a Chan inductor is not assigned, but is determined by its magnetic material, dimensional properties and winding turns, one must adjust inductance by iteratively adjusting the gap and/or winding turns. Measure inductancs by comparing slopes when subjected to the same stepped DC voltage.
- Parametize and wrap a Chan inductor with a subcircuit:
.subckt Core_Chan C params:
+ Bs=0.4 Br=0.1 Hc=20 ; Core default magnetic parameters
+ A=25u1 Lm=19m8 Lg=0m7 ; Core default physical parameters
+ Rp=10k Cp=10p ; Core default parallel loss and capacitance
Lc C 0 Rser=0 n=1 ; force Rser=0 and n=1
+ Bs={Bs} Br={Br} Hc={Hc}
+ A={A} Lm={Lm} Lg={Lg}
+ Rpar={Rp} Cpar={Cp}
.ends Core_Chan
- Chan Transformer Equivalent (Netlist Unprocessed):
Xp P 0 C Winding n=100 L=1u Rs=1m Rp=100 ; primary winding of 1:1 transformer Xs S 0 C Winding n=100 L=1u Rs=1m Rp=100 ; secondary winding of 1:1 transformer Xc C Core_Chan ; Chan inductor subcircuit with forced Rs=0 and n=1 + Bs=0.4 Br=0.1 Hc=20 Br=.10 ; Assigned core magnetic parameters + A=25u1 Lm=19m8 Lg=0m7 ; Assigned core physical parameters + Rp=10k Cp=10p ; Assigned core parallel loss and capacitance
Now how do I plot a B-H curve to see the Chan model's hysteresis-saturation curves?
Plotting hysteresis-saturation curves of the Chan Transformer in LTspice
Under construction.
1 ampere∙turn/meter = 4∙π/1000 Oersted(Oe)
1 volt∙seconds/turn/meter² = 1 Tesla(T) = 10,000 gauss(G)