Difference between revisions of "Transformers"
(Undo revision 393 by 85.10.193.108 (Talk)) |
m (→Transformers) |
||
| Line 7: | Line 7: | ||
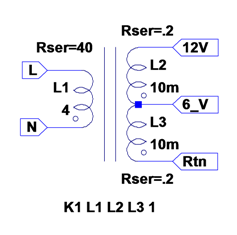
K1 L1 L2 L3 1 ; causes phasing dots to automatically appear on L1-L3 inductor symbols | K1 L1 L2 L3 1 ; causes phasing dots to automatically appear on L1-L3 inductor symbols | ||
| − | When creating a new transformer this way, especially for use in a switched-mode power circuit, it is generally best to first specify the mutual coupling coefficient to be exactly unity. By starting with 100 percent coupling there will be no leakage inductance in any winding and this will minimize the likelihood of the windings ringing at extremely high frequencies (which can slow the simulation to a crawl at each switching edge). However, be aware that a mutual inductance value of plus (or minus) unity ''may'' lead to simulation difficulties if ''Skip-the-initial-operating-point-solution'' (UIC) is specified for the .tran command. Prevent this by specifying a realistic resistance for each inductor "winding" (ctrl-right-mouse-click). Note that when coupled inductors are used as transformer windings, individual winding inductances rather than turns ratios must be specified (inductance ratios should be proportional to the '''''square''''' of the turns ratios). | + | When creating a new transformer this way, especially for use in a switched-mode power circuit, it is generally best to first specify the mutual coupling coefficient to be exactly unity. By starting with 100 percent coupling there will be no leakage inductance in any winding and this will minimize the likelihood of the windings ringing at extremely high frequencies (which can slow the simulation to a crawl at each switching edge). However, be aware that a mutual inductance value of plus (or minus) unity ''may'' lead to simulation difficulties if ''Skip-the-initial-operating-point-solution'' (UIC) is specified for the .tran command. Prevent this by specifying a realistic resistance for each inductor "winding" (ctrl-right-mouse-click). Note that when coupled inductors are used as transformer windings, individual winding inductances rather than turns ratios must be specified (inductance ratios should be set to be proportional to the '''''square''''' of the turns ratios). |
Revision as of 16:02, 21 October 2009
Transformers
How do I make a transformer in LTspice?
Although it is very possible to make a dedicated subcircuit for a specific transformer, the preferred method of making a generic transformer when drafting a simulation schematic is to simply place a separate inductor for each separate transformer winding and then couple them all together magnetically via a single Mutual Inductance (K) statement placed as a SPICE Directive on the schematic. Note that inductors called out in a Mutual Inductance statement will be automatically given a phasing dot if one does not already exist.
K1 L1 L2 L3 1 ; causes phasing dots to automatically appear on L1-L3 inductor symbols
When creating a new transformer this way, especially for use in a switched-mode power circuit, it is generally best to first specify the mutual coupling coefficient to be exactly unity. By starting with 100 percent coupling there will be no leakage inductance in any winding and this will minimize the likelihood of the windings ringing at extremely high frequencies (which can slow the simulation to a crawl at each switching edge). However, be aware that a mutual inductance value of plus (or minus) unity may lead to simulation difficulties if Skip-the-initial-operating-point-solution (UIC) is specified for the .tran command. Prevent this by specifying a realistic resistance for each inductor "winding" (ctrl-right-mouse-click). Note that when coupled inductors are used as transformer windings, individual winding inductances rather than turns ratios must be specified (inductance ratios should be set to be proportional to the square of the turns ratios).
I want to model leakage inductance - how should I do that?
The most flexible method is to keep the windings' mutual inductance statement at unity and add a small discrete leakage inductance in series with each winding. This is the most straightforward way to model transformers with asymmetrical leakage inductances. However, if your transformer is electrically symmetrical, it may be more convenient to simply set the mutual inductance to a value less than one. For each winding the resulting leakage inductance will be (1-K) times that winding's inductance. Note that each winding's coupled inductance also will decrease to K times that winding's inductance, but for typical values of K (>>0.9) this effect will be very small.
How about transformer saturation effects? Can LTspice model those?
Yes, LTspice comes with a non-linear hysteretic core model built in! This is the 1991 model by John Chan et al. Compared to older core models, the Chan model is particularly robust, computationally efficient and compact, requiring only three parameters to define most any commonly encountered magnetic hysteresis loop. (LTspice also allows building an arbitrary inductance based on self flux and/or any valid function of node voltages and branch currents. The arbitrary inductor model can be very efficiently used to create saturation without hysteresis.)
Once the core material's generic magnetic properties are set, establishing the circuit-level non-linear inductance requires specifying three more parameters to set the geometry of the specific core and specifying one additional parameter for the core winding turn-count. The Chan inductor does not currently directly support Mutual Inductance, so unless only a single-winding inductor is being modeled, multiple windings must be added via additional circuitry. The simplest way to do this is to construct an ideal, unity coupled transformer with as many windings as required and then put the Chan inductor directly in parallel with any one of the windings (taking care to set the turns to match that particular winding). Since the magnetic effects (including non-saturated inductance) are already modeled by the Chan inductor, the inductance of the transformer's parallel winding must be enough larger (>>10) not to significantly load the Chan inductance. As before, the inductances for the other windings should be scaled by the square of their individual turns ratios (with respect to the paralleled winding).
Okay, but calculating winding inductances is tedious. Is there some way to just enter a turns count for all the windings?
Yes, this can be done in any of a number of ways. For example, the values for each of the inductances may be directly parametrized via curly braces to be a function of turns ratios, or a subcircuit that accepts turns as a parameter may be used to encapsulate the windings implementation details. Below is a schematic of an LTspice circuit that is functionally equivalent to two mutually coupled inductors with arbitrary winding turns. Note how LTspice's fully extended inductor parasitics are included within this model. In this form (with a standard linear magnetizing inductance "core") the model is mostly useful as a perceptual window into the way coupled inductors work in LTspice.
Note that although this example has only two windings, any arbitrary number of windings are possible (just as with standard coupled inductors).
[This picture should be updated soon to agree with its following subcircuit. -- a.s.]
And here is its subcircuit representation in LTspice. Note that the magnetizing inductance "core" is the single summing point for the ampere-turns from all the windings and is the sole source of impressed voltage (=L*di/dt) reflected onto all the windings. Although this subcircuit is an unnecessary and overly complex representation for a transformer with a linear core inductance, it will be absolutely required if multiple windings are to be "wrapped" onto LTspice's nonlinear Chan inductance model, so take a moment to read it through (the Chan version will follow shortly).
.subckt Xfmr P1 P2 S1 S2 params:
+ Npri=300 Nsec=30 ; number of turns for primary and secondary (10:1)
+ L=1u K=0.95 ; single turn winding inductance and coupling factor
+ Rs=1u Rp=10 Cp=1u ; single turn series/parallel winding parasitics
*
* Derived Parameters
.param Lm=K*L Ls=(1-K)*L ; single turn magnetizing and leakage inductances
+ Np2=Npri**2 Ns2=Nsec**2 ; turns squared for primary and secondary
*
* Primary Winding (Np turns)
Cp P1 P2 {Cp/Np2} Rpar={Rp*Np2} ; parallel capacitance and resistance
Lp P1 n1 {Ls*Np2} Rser={Rs*Np2} ; series leakage inductance and resistance
Ep n1 n2 n3 0 {Np} ; reflected magnetizing voltage = L*di/dt
Vp n2 P2 0 ; primary winding current sense
* Magnetizing Inductance (1 turn)
Fp 0 n3 Vp {Np} ; ampere-turns reflected from primary winding
Lm 0 n3 {Lm} Rser=0 ; ideal magnetizing inductance (for 1 turn)
Fs 0 n3 Vs {Ns} ; ampere-turns reflected from secondary winding
* Secondary Winding (Ns turns)
Vs n4 S2 0 ; secondary winding current sense
Es n5 n4 N3 0 {Ns} ; reflected magnetizing voltage = L*di/dt
Ls S1 n5 {Ls*Ns2} Rser={Rs*Np2} ; series leakage inductance and resistance
Cs S1 S2 {Cp/Ns2} Rpar={Rp*Np2} ; parallel capacitance and resistance
.ends Xfmr
And here is the same thing using parameters within curly braces to give value to LTspice's extended inductors and to a coupling statement (mutual inductance). Note that there is no need to create a subcircuit with this method because Lp and Ls can be placed directly on the schematic as symbols and K1 and the .param statement may be placed as SPICE text (this is the section of netlist that would then result). The prior subcircuit form (or something like it) only becomes necessary in conjunction with a custom two-winding transformer symbol or if a nonlinear core (magnetizing inductance) model must be used.
.param Npri=300 Nsec=30 L=1u K=0.95 Rs=1u Rp=10 Cp=1u
+ Np2=Npri**2 Ns2=Nsec**2 ; turns squared for primary and secondary
Lp P1 P2 {L*Np2} Rser={Rs*Np2} Rpar={Rp*Np2} Cpar={Cp/Np2}
Ls S1 S2 {L*Ns2} Rser={Rs*Ns2} Rpar={Rp*Ns2} Cpar={Cp/Ns2}
K1 Lp Ls {K}
Knowing the internal workings of LTspice's coupled inductor style transformer is all very interesting, but how do I make something that uses separate standard inductor symbols for winding, yet also uses the Chan core model with full saturation and hysteresis?
The following method allows this:
File:Separate Winding.png [obviously, this section is not yet complete]
This model uses the standard inductor symbol edited to appear as a winding subcircuit on a core (connected through a global node). The core may be linear or nonlinear (e.g., LTspice's built in Chan model) and may have as many windings as required. Due to the use of a global core node (which must be different for each core), a different subcircuit is required for each core.